Qu'est-ce que les mathématiques ?

• Introduction
• C’est quoi, faire des maths ?
• Pourquoi on utilise des lettres en maths ?
• A quoi ça sert les maths ?
• Pourquoi on parle de “beauté” en maths ?
• Donc c’est une science ou pas ?
• Notes de bas de page

Introduction

Comme je l’ai évoqué dans ce billet, je souhaitais écrire un billet de blog sur quelques disciplines pour en détailler les méthodologies et répondre à la fameuse question : “sont-elles des sciences ?”. C’est donc naturellement que je commence par ma discipline préférée, celle où j’ai un peu d’expertise : les mathématiques !
Toutefois, et cela va vite être clair pour le lecteur, la nature même des mathématiques font que la question n’est pas vraiment intéressante. Elles ont une place à part au sein des connaissances humaines de sorte que savoir s’il faut les qualifier de science ou non n’est pas très important.
Ainsi, ce billet sera simplement mon pretexte pour parler de mathématiques, et répondre aux questions qu’on m’a toujours posé dessus.

C’est quoi, faire des maths ?

Le but des mathématiques est de démontrer des énoncés mathématiques. La question qui suit est bien entendu : que signifie démontrer ? C’est ce que je vais expliquer dans cette section, en proposant au lecteur de faire lui-même ce qui sera peut-être sa première démonstration mathématique. Mais pas de panique, on va l’enrober de telle sorte qu’on n’aura même pas l’impression de faire des maths, on va plutôt parler de peinture.

Imaginons avoir devant nous un ensemble de peintures de différentes couleurs. Cette peinture est une peinture spéciale qui ne se mélange pas comme la peinture classique. Mélanger du rouge et du bleu donnera toujours la même couleur, mais ce n’est peut-être pas du violet ! C’est peut-être du vert ou du noir, à priori on ne le sait pas. Peut-être même qu’avec cette peinture spéciale, mélanger du orange avec du orange donne autre chose que du orange !
Imaginons aussi qu’il existe au moins une couleur qui, lorsqu’on la mélange avec les autres, ne les modifie pas. On dit que cette couleur est neutre. Une couleur neutre mélangée au rouge est encore rouge, et mélangée au bleu donne du bleu. Ces hypothèses ne sont certes pas très réalistes mais ce n’est pas très important, on va simplement se poser la question suivante : Peut-il exister deux couleurs neutres différentes ?

La réponse n’est pas si difficile à trouver, si le lecteur veut essayer par lui-même, il peut faire une pause ici.

Figure 1. Un exemple où mélanger le jaune et le bleu donne du rouge plutôt que du vert.

Voici comment répondre à la question. Partons du principe que oui, il existe deux couleurs neutres différentes. Imaginons pour fixer les idées qu’il s’agisse du vert et du orange. Alors, que se passe-t-il en mélangeant le vert et le orange ? Le vert est neutre, il n’altère donc pas le orange, et le mélange reste orange. Mais le orange aussi est neutre, il n’altère donc pas le vert, et le mélange reste vert ! C’est impossible, et comme notre raisonnement marcherait pour toutes les couleurs (pas seulement pour le vert et l’orange) notre hypothèse est fausse. On conclut alors qu’il ne peut pas exister deux couleurs neutres différentes.

La démonstration est terminée. On peut constater que ce n’est pas un exercice très différent de celui de résoudre une énigme, comme on peut en trouver des centaines ici par exemple. Dans les deux cas, l’idée est d’utiliser la logique pour montrer qu’un énoncé mathématiques est forcément vrai (ou forcément faux).

A présent élevons un peu la difficulté. On vient de voir qu’il existe une unique couleur neutre (c’est-à-dire qui n’altère pas la couleur avec laquelle on la mélange), dont pour simplifier on va dire qu’il s’agit du blanc. J’ajoute maintenant la règle suivante : pour chaque couleur, il existe une couleur inverse, c’est-à-dire une couleur qui, mélangée à la première, donne la couleur neutre blanche. Par exemple le rouge et son inverse (peut-être du vert, ou du jaune, je ne le précise pas) donnent du blanc¹. Ma deuxième question est la suivante : Quelles sont les couleurs qui ne changent pas lorsque je les mélange avec elle-même ?

A nouveau, la réponse n’est pas très difficile à trouver, si le lecteur veut essayer par lui-même, il peut faire une pause ici².

La solution est celle-ci. Prenons une couleur qui ne change pas lorsque je la mélange avec elle-même, et pour simplifier imaginons qu’il s’agisse du rouge. Faisons un mélange avec trois couleurs : du rouge, du rouge et l’inverse du rouge.

• Comme le rouge et le rouge donnent du rouge, cela revient à mélanger du rouge avec l’inverse du rouge : on obtient la couleur neutre.
• Mais comme le rouge et l’inverse du rouge donnent la couleur neutre, cela revient à mélanger le rouge avec la couleur neutre : on obtient du rouge.

On vient de montrer que la couleur rouge est la couleur neutre, donc la seule couleur qui ne change pas lorsque je la mélange avec elle-même, c’est la couleur neutre !

Pourquoi on utilise des lettres en maths ?

Cette dernière démonstration était un peu plus difficile que la première. On devait penser à faire le mélange “rouge/rouge/inverse” et l’étudier de deux façons différentes. Et on pouvait facilement s’embrouiller avec toutes les couleurs en jeu et leurs propriétés contre-intuitives. En plus, écrire tout ça en français est assez rébarbatif.
C’est justement pour simplifier et clarifier leurs raisonnement que les mathématiciens utilisent des lettres. Pour expliquer comment ce langage mathématiques est codé, je vais réécrire la démonstration précédente comme un mathématicien l’écrirait. Les parties mathématiques seront surlignées, pour les distinguer de mes commentaires destinés au lecteur.

Tout d’abord on doit définir les lettres, qui font office d’abbréviations :

• l’élément neutre sera noté $n$,
• la couleur qui reste la même lorsqu’on la mélange avec elle même sera notée $x$,
• l’inverse d’une couleur $x$ est notée $x^{-1}$,
• l’action de mélanger sera notée avec un point $\cdot$, c’est-à-dire que la couleur qu’on obtient lorsqu’on mélange une première couleur (notée $y$) avec une seconde couleur (notée $z$) sera notée $y\cdot z$.

Ensuite on peut commencer la preuve.
On sait que $x\cdot x = x$ , car $x$ représente une couleur qui ne change pas par le mélange “$\cdot$” avec elle même.
Donc ajoutant l'inverse en déduit que $x^{-1}\cdot x \cdot x = x^{-1}\cdot x$, les deux côtés de l’équation représentent la même couleur, donc l’équation reste vraie si si on ajoute le $x^{-1}$ des deux côtés de l’équation.
Or $x^{-1}\cdot x = n$ et $n\cdot x = x$, par définition $x^{-1}$ est l’inverse de $x$, donc en les mélangeant on obtient la couleur neutre $n$.
Donc $x=n$.

On voit que la preuve est bien plus courte (et un mathématicien ferait encore bien plus court), et le langage symbolique permettent d’y voir plus clair que dans des lignes de mots en français ! Ce qu’il faut retenir est donc qu’on peut faire des maths sans symboles et autres lettres, c’est d’ailleurs comme ça que les maths étaient écrites historiquement, mais ils sont tellement utiles qu’on est très vite limités si on ne les utilise pas.

A quoi ça sert les maths ?

Je vois trois façons de répondre à cette question.

La première serait de mettre en évidence que les mathématiques s’appliquent dans tous les domaines de la vie moderne.
Pour appeler quelqu’un par téléphone, il a fallu des mathématiques pour écrire le code informatique qui permet au téléphone de fonctionner. Le fonctionnement des transistors, qui sont la brique fondamentale de tout appareil électronique, repose sur de la physique (l’électromagnétisme voire la mécanique quantique) qui a été écrite dans un langage mathématiques très complexe. Idem pour le satellite avec lequel communique le téléphone, il a été mis en orbite grâce à la mécanique newtonienne et doit prendre en compte la relativité pour fonctionner : toute cette physique comporte des mathématiques très poussées.
Pour faire une raido des poumons après suspicion de pneumonie d’origine bactérienne ? Il a fallu de la physique (donc des mathématiques) pour concevoir la radio. On utilise des modèles mathématiques pour suivre comment la maladie se répand dans la population. On utilise les statistiques pour s’assurer que le traitement qu’on donne n’est pas dangereux.
Pour estimer le juste prix d’une assurance (le prix qu’il faut payer pour égaler en moyenne ce qu’il va falloir rembourser), il faut des statistiques et des probabilités.
Enfin, il faut savoir que la sécurité de toutes nos transactions bancaires et de l’internet lui-même repose sur un algorithme et des propriétés arithmétiques, le protocole RSA.

Une deuxième façon de répondre est de dire que faire des mathématiques, c’est faire de l’exercice intellectuel. De la même manière qu’aller à la salle de sport sert à prendre soin de son corps, faire des maths servirait à prendre soin de son cerveau.
On pourrait même aller un peu plus loin et ajouter qu’avoir des bases en mathématiques est utile pour comprendre des concepts qu’un citoyen éclairé se doit de connaître. Je pourrais penser par exemple à la notion d’exponentielle qu’on a beaucoup rencontrée pendant le Covid, mais qui intervient aussi lorsqu’on parle d’épargne financière à travers la notion d’intérêts composés. Ou bien à la notion de dérivée qui est au coeur de la différence entre flux et stock et qui est nécessaire de comprendre si on veut maitriser des nuances fondamentales entre les concepts de PIB, dette publique, croissance économique, inflation, patrimoine financier, etc… dont les JT et les discours politiques sont parsemés.

Mais il me semble que la meilleure manière de répondre est la troisième. Sans négliger l’importance des deux premiers points, ce n’est pas pour ces raisons que j’ai fait des mathématiques mon métier. Pour moi, l’intérêt des mathématiques est double. D’une part les démonstrations mathématiques donnent aux mathématiciens la certitude du résultat obtenu. Ceci est très différent des autres disciplines scientifiques, où les résultats ont des marges d’erreur (par exemple en médecine), où on peut imaginer que les théories les plus solides soient rendus caduques par des découvertes ultérieures, et où les objets étudiés contraignent les scientifiques dans leur étude (par exemple en économie ou en sociologie)³. Cette certitude permet d’avancer dans son travail sans se demander sans cesse si les propositions sur lesquelles on s’appuie sont vraiment solides, et elle m’a souvent manqué lorsque je me suis intéressé à d’autres disciplines comme la physique. D’autre part, ces vérités sont universelles, dans le sens où on découvre des choses fondamentales qui sont vraies pour toujours et partout dans l’Univers. Le mathématicien cherche d’ailleurs à faire les découvertes les plus générales possibles, et cette recherche d’abstraction ne rend pas les mathématiques moins concrètes. Au contraire, bien que ses résultats soient formels (c’est-à-dire contenus dans nos tableaux noirs et feuilles blanches) ces généralisations élargissent les champs d’application possibles.

Pourquoi on parle de “beauté” en maths ?

Une dernière raison pour laquelle on fait des mathématiques, c’est qu’elles sont souvent belles. Je sais que lorsque j’utilise ce mot, je passe probablement pour un illuminé ! J’ai d’ailleurs pu lire un jour, La beauté en maths, soit t’es matheux, tu sais ce que c’est, et j’ai pas besoin de te l’expliquer ; soit t’es pas matheux, tu ne vois pas ce que c’est, et je ne peux pas te l’expliquer. Et pourtant, je ne suis pas d’accord, je pense qu’il est facile de faire comprendre ce qu’on entend lorsqu’on parle de beauté en mathématiques.

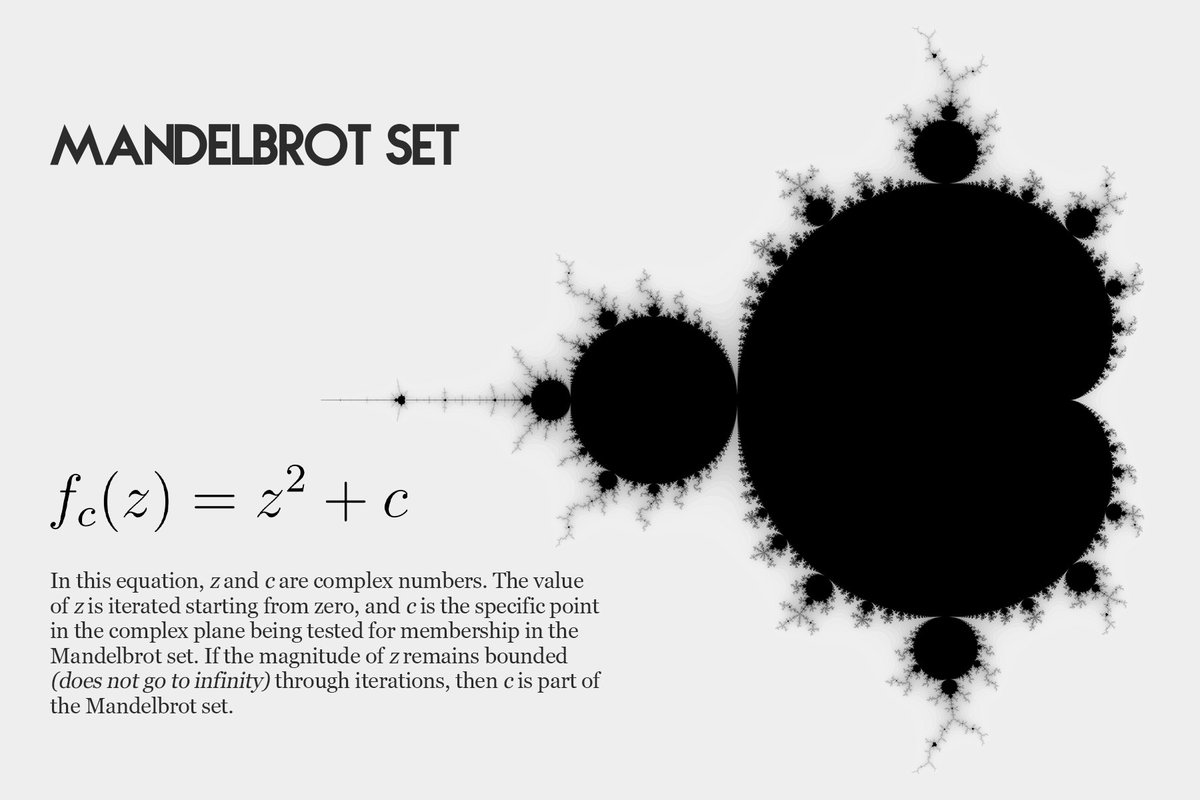
La première, la plus simple, est de tout simplement montrer à quoi ressemblent certains objets sont sortis de l’esprit de mathématiciens. Je pense à l’ensemble de Mandelbrot ou l’ensemble de Julia, qu’on peut observer dans cette vidéo, et dont je mets une image du premier dans la Figure 2. Sans même se demander ce dont il s’agit, n’est-ce pas beau ?

Figure 2. Le fameux ensemble de Mandelbrot.

Mais lorsque les mathématiciens parlent de beauté, la plupart du temps ils ne parlent pas des objets qu’ils manipulent, mais des raisonnements qu’ils font. Et ça c’est plus difficile à expliquer, mais je vais quand même tenter. Au début de ce billet j’évoquais l’idée que faire une démonstration était assez proche de résoudre une énigme. Ceux qui aiment ça voient peut-être où je veux en venir, certaines solutions sont élégantes car on se dit “c’était facile, il suffisait d’y penser !”. De la même manière, les mathématiciens parlent de beauté en maths comme les lecteurs de roman policier parlent des déductions de Sherlock Holmes ou les amateurs d’échecs décrivent les plus beaux coups aux échecs.

Pour finir, je vais présenter une troisième démonstration, que je vais faire de deux manières différentes. La première ne sera pas élégante, mais la deuxième le sera de façon à rendre palpable pour le lecteur ce que cette nuance signifie. On va essayer de résoudre le problème suivant : Prenons un présentoir de forme triangulaire sur lequel est posé une chaine de perles dont la longueur est telle qu’elle repose entièrement sur les deux côtés du dessus du triangle. Cette disposition est représentée en Figure 3.1. La chaîne va-t-elle glisser sous l’effet de son poids, et si oui de quel côté ?

Figure 3.1. La situation du problème. La chaine de perle repose sur le dessus du triangle.

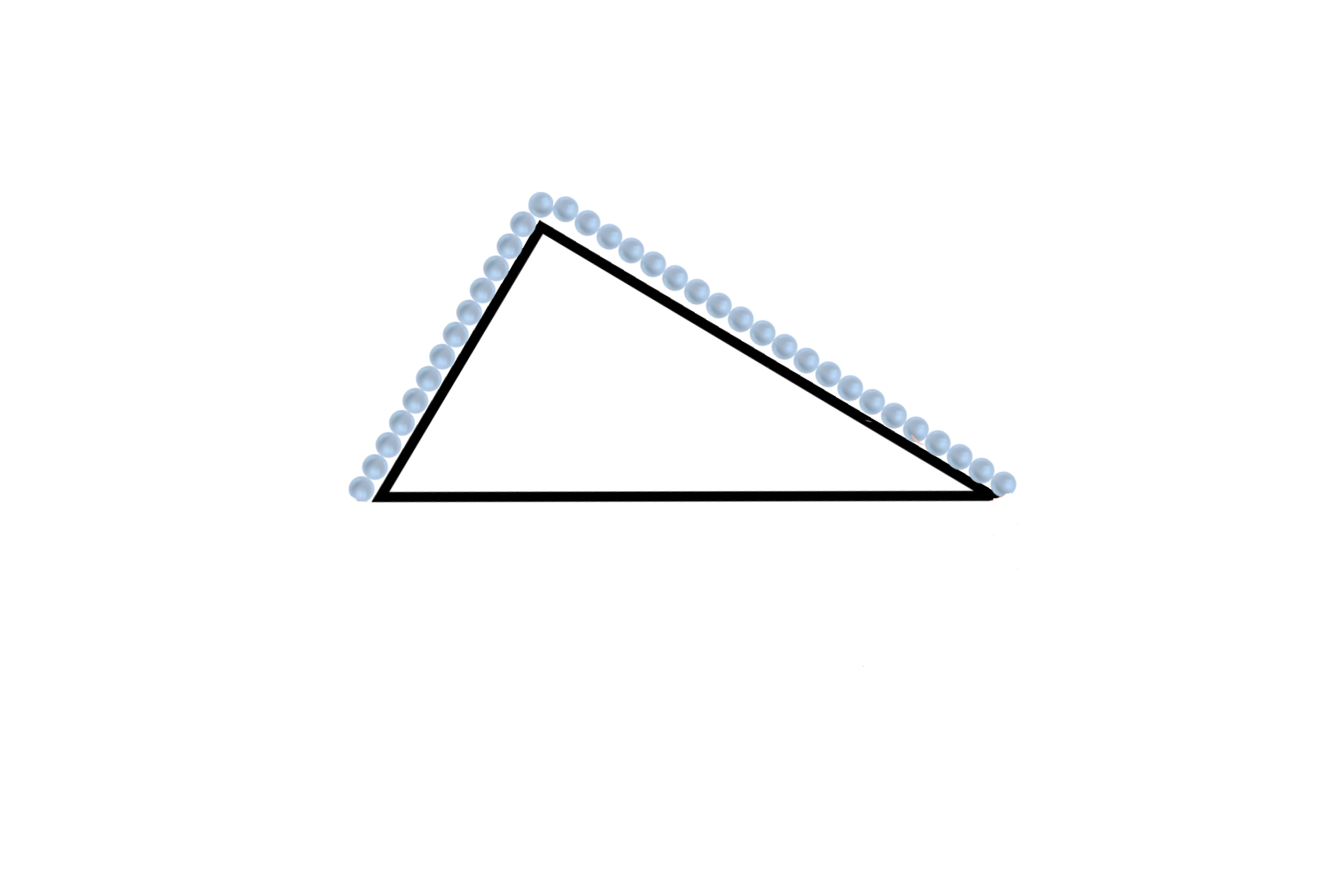
La première façon de résoudre ce problème est par la force brute. Pas besoin de réfléchir, c’est un problème classique de mécanique statique dont on peut utiliser les outils ainsi que des formules de trigonométrie. L’objectif sera de calculer la force appliquée au sommet du triangle par la partie gauche de la chaîne, faire de même pour la partie droite de la chaîne, et regarder quelle force est la plus grande et enfin en déduire de quel côté glissera la chaîne. Tout ceci doit être calculé en fonction des longueurs ou angles possibles pour le triangle. Je ne vais pas le faire car ce serait fastidieux et inutile dans le cadre de ce billet. Mais comme j’imagine que faire cet exercice n’enthousiasmerait peu de lecteurs, celui-ci conviendra que la démonstration est tout sauf élégante.

L’autre façon de résoudre le problème est de penser à une astuce qui simplifierait énormément le problème. Imaginons maintenant non pas une chaîne posée sur le triangle, mais un collier qui en fasse le tour, comme sur la Figure 3.2. Le collier est constitué de deux parties.

• La première, en bleu sur la Figure 3.1, est la même chaine que dans la version précédente.
• La seconde, en rouge sur la Figure 3.2, est suspendue aux deux extremités du triangle.

Il est facile de se convaincre que la partie suspendue en rouge ne tire pas plus d’un côté que de l’autre et ne contribue pas à faire bouger l’ensemble du collier. Le collier entier non plus ne va pas se mettre à tourner spontanément. On en déduit donc facilement que la chaine bleue ne bouge pas non plus, sinon elle entrainerait le collier entier avec elle.

Figure 3.2. L'astuce consiste à ajouter la chaine rouge pour former un collier qui entoure le triangle.

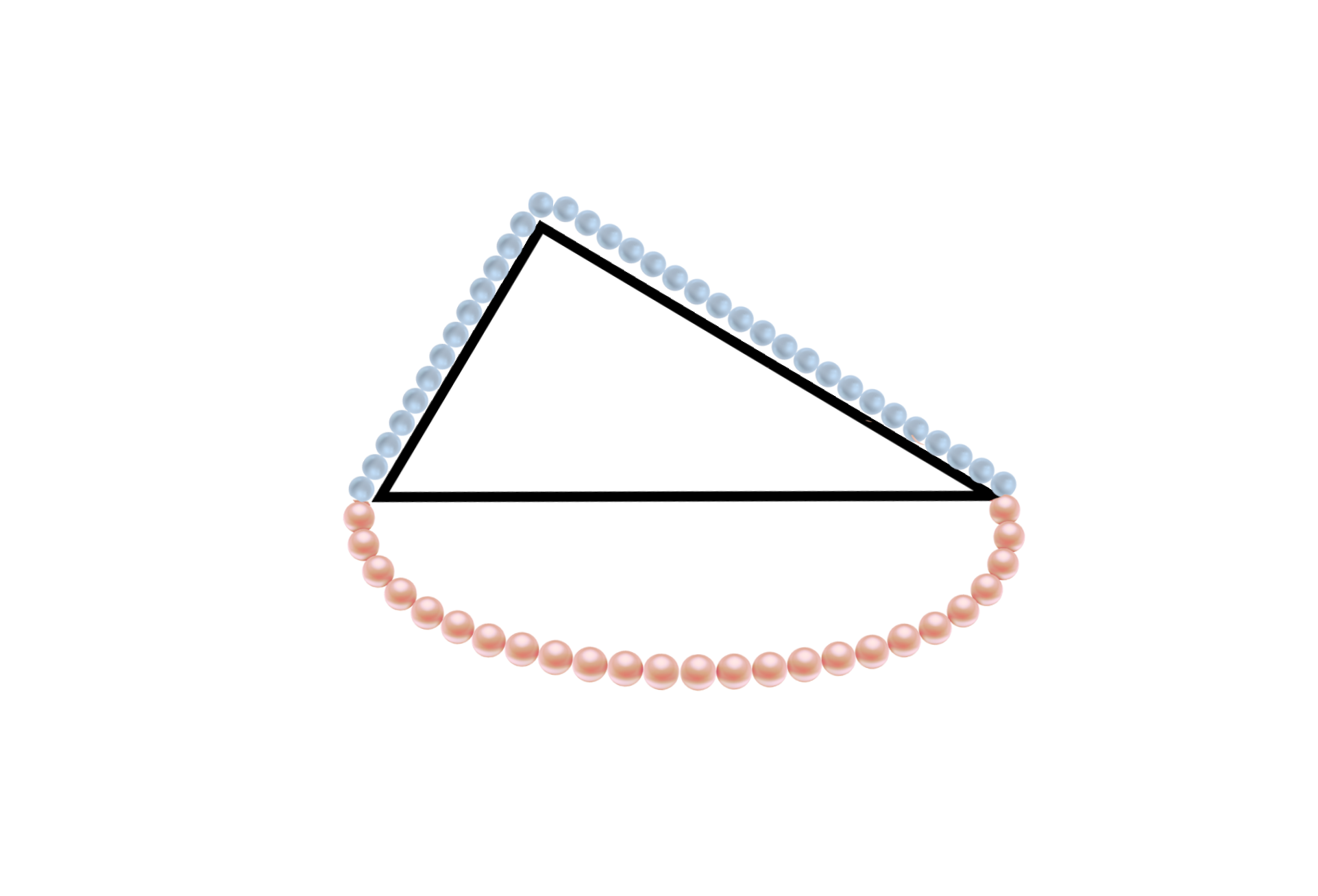
La démonstration est donc terminée ! La chaine ne glisse d’aucun des côtés du triangle. Le fait d’avoir pensé à l’astuce du collier nous a épargné de longs calculs, et c’est ça qui fait l’élégance de la démonstration. Une démonstration est belle, entre autres, lorsqu’elle est ingénieuse et simple.

Donc c’est une science ou pas ?

Comme on l’a vu, les mathématiques ont un statut épistémique assez spécial.

D’une part, le travail du mathématicien est abstrait, théorique. La recherche en mathématiques est parfois guidée par des questions d’élégance totalement déconnectées du monde réel, comme ça a par exemple été le cas pour la découverte des nombres complexes⁴. Ainsi, et contrairement aux autres sciences, la notion de vérité en mathématiques n’est pas vraiment liée à l’adéquation entre une théorie et le monde réel.

D’autre part, si on devait mesurer la qualité d’une science à la certitude qu’elle apporte envers les propositions qu’elle contient⁵, les mathématiques seraient la science ultime : on ne peut pas mieux justifier une affirmation que ne le font les mathématiciens.

De ce fait, les mathématiques sont inclassables au sein des disciplines scientifiques, elles sont plus à rapprocher de la philosophie que de la physique.

Notes de bas de page